Implementing 4D PGA into XPBD
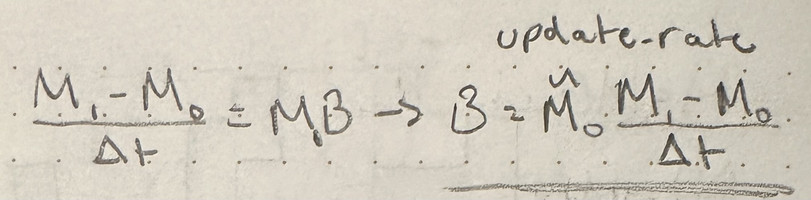
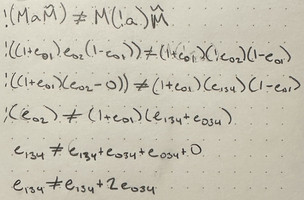
January 25, 2025 Update
This is OUTDATED! I chose to instead implement a 4D physics engine by following this paper: https://marctenbosch.com/ndphysics/NDrigidbody.pdf
I probably could have made XPBD + 4D PGA work if I changed the integration scheme to something that was less likely to diverge like semi-implicit Euler. Although you would still be met with the challenge of getting update_rate to agree with that scheme. In other words, basic euler integration easily blew up to infinity, but update_rate computed rate by solving for rate inside the basic equations. If update_rate solves for rate in way that isn't derived from the integrate equations then rotation and translation gets coupled.
Previous blog post unchanged:
This is in no way an exhaustive list of all of the problems I ran into, but I wanted to list out some of the more memorable ones. Also when I was looking into using 4D PGA, I started off trying to implement it using the rust code generated at https://bivector.net/tools.html?p=4&q=0&r=1 and from what I knew about PGA from watching sudgylacmoe's videos and having implemented GA a little bit before. I wasn't really getting anywhere, until I found the resources at https://bivector.net/doc.html. Note: A lot of the problems I had probably could have been avoided by me properly learning this stuff before trying to implement it.
Changing XPBD:
For XPBD I had followed https://johanhelsing.studio/posts/bevy-xpbd up to and including part 4, so I had, on my own, added an orientation component that used a Mat4, however there was still no rotational velocity. I had also generalized the shapes to use the same geometry builder as the manifold so I could write the contact solver more generally (although only hyperspheres can currently be dynamic).
Since position and rotation is combined, some of the stored quantities have different names:
- Pose (Motor) = position + orientation
- Rate (Bivector) = velocity + angular velocity
- Momentum/Impulse (Dual of bivector) = momentum + angular momentum
- Acceleration (Bivector) = acceleration + angular acceleration
- Forque (Dual of bivector) = force + torque
- Inertia (Map from a bivector to the dual of a bivector) = mass + moment of intertia
Some problems I ran into:
- Duality operator: the file by default implemented the Poincare duality operator, while it seems like most PGA equations use the hodge star definition. These are mostly the same, except for a bunch of negative signs. I implemented it how it is described here.
- Compute rate from pose and prev_pose: This wasn't a given equation since it isn't usually needed, so I just manipulated the equation relating M0, M1, Δt, B. Note that ~M0 is on the left, since the geometric product isn't necessarily commutative, this is important.
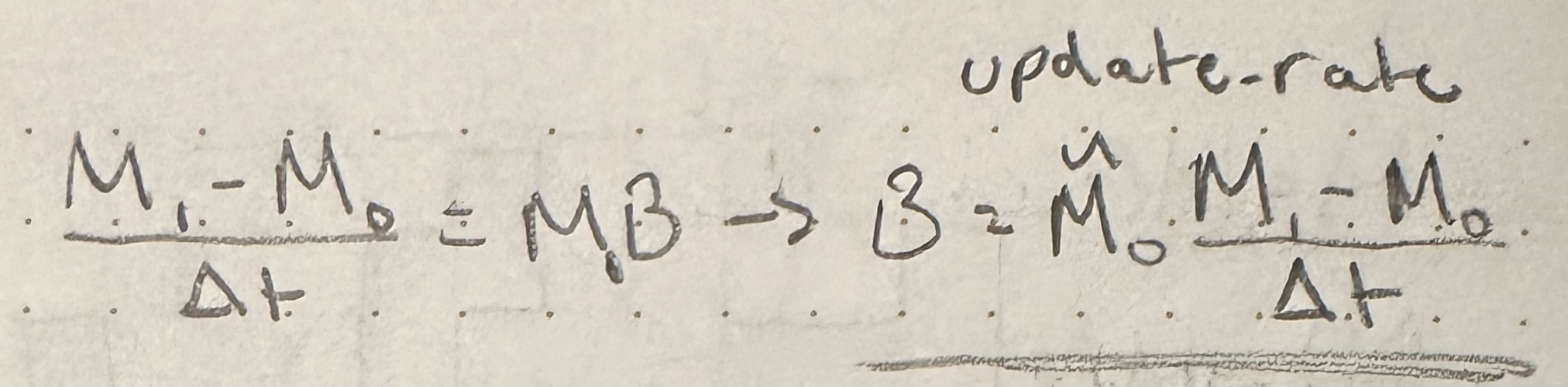
- Computing restitution: I, stupidly, was trying to use the restitution equation provided in "May the Forque be with you" for solve_rate even though XPBD computes restitution differently
- From what I know of XPBD right now collisions work like this:
- solve_pose: Will compute the impulse that will separate the two objects and applies that impulse directly to pose
- update_rate: This always runs regardless of collisions, sets the rate to match the change in pose
- solve_rate: Undoes that change in rate caused by the solve_pose and updates the rate with the computed restitution impulse. The reason I'm using the dot product on multivectors is to try and calculate the relative impact that the two object's inertias have on the collision. I have no clue if this is the correct way to do this.
- Current solve_rate (probably still somewhat incorrect):
fn solve_rate( mut query: Query<(&Pose, &mut Rate, &PrevRate, &Inertia, &Restitution), Without<isstatic>>, contacts: Res<contacts> ) { for (entity_a, entity_b, contact) in contacts.0.iter().cloned() { let ( (pose_a, mut rate_a, prev_rate_a, inertia_a, restitution_a), (pose_b, mut rate_b, prev_rate_b, inertia_b, restitution_b), ) = query.get_pair_mut(entity_a, entity_b).unwrap(); let n = contact.normal; let restitution = (restitution_a.0 + restitution_b.0) / 2.0; let normal_rate: Bivector = (n.x * e01 - n.y * e02 + n.z * e03 - n.w * e04).into(); let prev_relative_a: Bivector = (prev_rate_a.mv() - pose_a.inverse().apply(pose_b.0.apply(prev_rate_b.mv()))).into(); let prev_relative_b = (prev_rate_b.mv() - pose_b.inverse().apply(pose_a.0.apply(prev_rate_a.mv()))).into(); let relative_a = (rate_a.mv() - pose_a.inverse().apply(pose_b.0.apply(rate_b.mv()))).into(); let relative_b = (rate_b.mv() - pose_b.inverse().apply(pose_a.0.apply(rate_a.mv()))).into(); rate_a.0 += 0.5 * -normal_rate * (normal_rate.dot(relative_a) + (restitution * normal_rate.dot(prev_relative_a)).min(0.0)); rate_b.0 -= 0.5 * -normal_rate * (normal_rate.dot(relative_b) + (restitution * normal_rate.dot(prev_relative_b)).min(0.0)); } }
- From what I know of XPBD right now collisions work like this:
- How to store multivectors: Multivectors in 4D PGA have 32 components and are therefore representable as [f32; 32], but I chose to create a macro that makes a struct that stores a subset of this.
- Since most values are specific subsets of a full multivector (a bivector is the 2-grade component, a motor is the even grade components), I felt it made more sense to store these subsets as different structs. Although, since I didn't want to re-implement multiplication, pretty much all mathematical operations have to convert to multivectors first, then convert back (which isn't ideal)
- This ended up with an annoying amount of .into()
- This isn't fully fleshed out, but you could use typestate programming to do the minimum amount of computation at each step while storing the smallest amount possible: typestate ga example, I don't know what the performance for this would look like.
- If I were to do this again, I probably would have just kept everything as a multivector since my game is gpu-bound anyway.
- Here is the macro if you want to see/use/add to it:
macro_rules! define_component { ($name:ident, $size:literal, [$($index:literal),*]) => { #[derive(Debug, Clone, Reflect, Copy, Default)] pub struct $name(pub(crate) [f32; $size]); impl $name { pub const ZERO: $name = $name([$(0.0 * ($index as f32),)*]); pub fn dot(&self, rhs: Self) -> f32 { let a = self.mv(); let b = rhs.mv(); $(a[$index] * b[$index] + )* 0.0 } } impl std::fmt::Display for $name { fn fmt(&self, f: &mut Formatter<'_>) -> std::fmt::Result { write!(f, "{}({})", stringify!($name), R401::from(self.clone())) } } impl From<r401> for $name { fn from(value: R401) -> Self { $name([$(value[$index],)*]) } } impl From<$name> for R401 { fn from(value: $name) -> Self { let mut mv = R401::zero(); [$(mv[$index],)*] = value.0; mv } } impl<t> std::ops::Mul<t> for $name where T: Into<r401> { type Output = Self; fn mul(self, rhs: T) -> Self::Output { (R401::from(self) * rhs.into()).into() } } impl std::ops::Mul<$name> for f32 { type Output = $name; fn mul(self, rhs: $name) -> Self::Output { (R401::from(rhs) * self).into() } } impl<t> std::ops::Add<t> for $name where T: Into<r401> { type Output = Self; fn add(self, rhs: T) -> Self::Output { (R401::from(self) + rhs.into()).into() } } impl<t> std::ops::AddAssign<t> for $name where T: Into<r401> { fn add_assign(&mut self, rhs: T) { *self = (R401::from(*self) + rhs.into()).into() } } impl<t> std::ops::SubAssign<t> for $name where T: Into<r401> { fn sub_assign(&mut self, rhs: T) { *self = (R401::from(*self) - rhs.into()).into() } } impl std::ops::Neg for $name { type Output = $name; fn neg(self) -> Self::Output { self * -1f32 } } } } define_component!(Motor, 16, [0, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 26, 27, 28, 29, 30]);
- World vs. Body Frame: I think that this is most likely the source of my current problems. Also, now that I am looking more closely at this cube on a string example I am realizing that
!(M >>> a)(eq. 1) does not equalM >>> !a(eq. 2) where ! is the hodge star dual, and >>> is the sandwich product. - Here is an example of the two eqs producing different results for a = 1e02 and M = 1 + e01
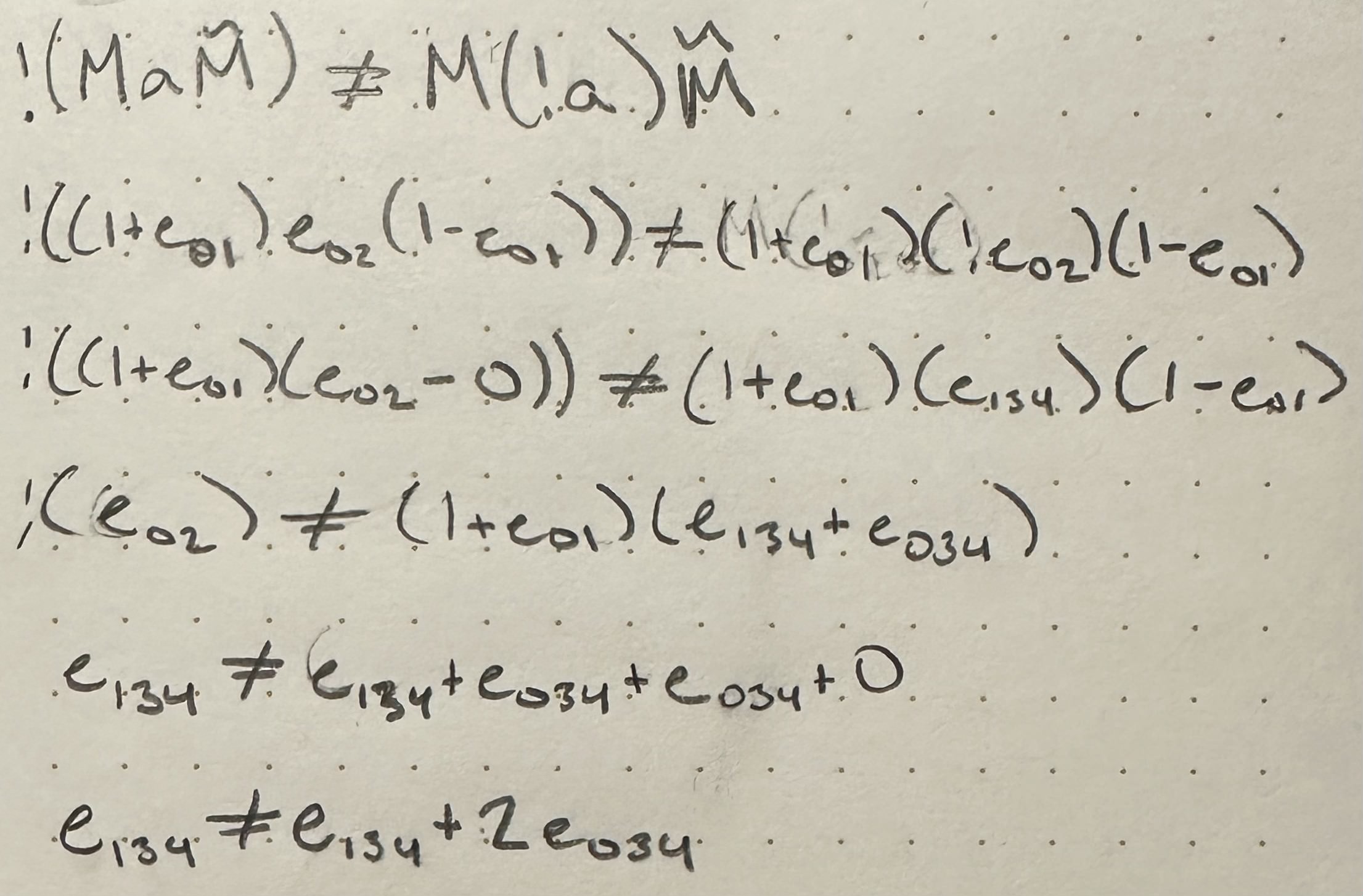
- Pose constraints: In order to have the physics work on the surface of a 4D object, it needs to be constrained to it at every substep, both in position and orientation. Constraining position is easy, but since the physics for rotation hasn't been working I haven't been able to test constraining the orientation part of pose.
- I'll continue to update this page as I work on it or remember issues that I ran into
Moving Forwards
My plan, as of right now, is to eventually continue with 4D PGA after I work on some other features, hoping that when I go back to the code with a fresh mind I'll be able to fix it up. If that doesn't work out, I have a two alternatives in mind:
- Use 4D VGA Rotors: Rotors can represent rotations in any amount of dimensions so I could just use those for everything rotation-related and keep the position physics basic.
- Use a 4D vector: Since all of the rotation should be happening within the 3D surface of the 4D object, I could be representing rotation as happening around the plane created by the normal to the surface and the 4D vector, with the magnitude of the vector representing rotational speed.
R401.rs:
Currently the R401.rs file generated on bivector.net does not compile, the version that I edited and am now using is below. Although the current code generator in the ganja.js repo does work: codegen.
For the things that need to be fixed, it's easiest if you can do find/replace with regex:
- All of the consts are private
- for the consts that you want to use, you need to find/replace the "const" with "pub const".
- Also R401 is private so you need to make it public
- IMPORTANT: often in PGA physics the equations will use the hodge star definition of duality, and here the poincare definition is used
- They are the same except for some negative signs, to find the sign for a basis, use the sign of: the basis * (poincare dual of that base)
- Example: e01 * (poincare dual of e01) = e01 * e234 = e01234 => hodge star of e01 = +e234
- or just watch this
- In the regressive product definition, integers and floats are being multiplied, this makes rust angry
- Use the regex:
(?<=[\+\-*])(\d)|(\d)(?=[\+\-*])and substitute with$1.0to fix this
- Use the regex:
- This is a matter of taste, but I made all of the methods all lowercase
// Written by a generator written by enki. (edited by tomwol)
#![allow(unused_imports)]
#![allow(dead_code)]
#![allow(non_upper_case_globals)]
#![allow(non_snake_case)]
#![allow(non_camel_case_types)]
use std::fmt;
use std::ops::{Index, IndexMut, Add, Sub, Mul, BitAnd, BitOr, BitXor, Not, Neg, Div};
type float_t = f32;
// use std::f64::consts::PI;
const PI: float_t = 3.14159265358979323846;
const basis: &'static [&'static str] = &[ "1","e0","e1","e2","e3","e4","e01","e02","e03","e04","e12","e13","e14","e23","e24","e34","e012","e013","e014","e023","e024","e034","e123","e124","e134","e234","e0123","e0124","e0134","e0234","e1234","e01234" ];
const basis_count: usize = basis.len();
#[derive(Default,Debug,Clone,Copy,PartialEq)]
pub struct R401 {
mvec: [float_t; basis_count]
}
impl R401 {
pub const fn zero() -> Self {
Self {
mvec: [0.0; basis_count]
}
}
pub const fn new(f: float_t, idx: usize) -> Self {
let mut ret = Self::zero();
ret.mvec[idx] = f;
ret
}
pub const fn with(mut self, f: float_t, idx: usize) -> Self {
self.mvec[idx] = f;
self
}
}
// basis vectors are available as global constants.
pub const e0: R401 = R401::new(1.0, 1);
pub const e1: R401 = R401::new(1.0, 2);
pub const e2: R401 = R401::new(1.0, 3);
pub const e3: R401 = R401::new(1.0, 4);
pub const e4: R401 = R401::new(1.0, 5);
pub const e01: R401 = R401::new(1.0, 6);
pub const e02: R401 = R401::new(1.0, 7);
pub const e03: R401 = R401::new(1.0, 8);
pub const e04: R401 = R401::new(1.0, 9);
pub const e12: R401 = R401::new(1.0, 10);
pub const e13: R401 = R401::new(1.0, 11);
pub const e14: R401 = R401::new(1.0, 12);
pub const e23: R401 = R401::new(1.0, 13);
pub const e24: R401 = R401::new(1.0, 14);
pub const e34: R401 = R401::new(1.0, 15);
pub const e012: R401 = R401::new(1.0, 16);
pub const e013: R401 = R401::new(1.0, 17);
pub const e014: R401 = R401::new(1.0, 18);
pub const e023: R401 = R401::new(1.0, 19);
pub const e024: R401 = R401::new(1.0, 20);
pub const e034: R401 = R401::new(1.0, 21);
pub const e123: R401 = R401::new(1.0, 22);
pub const e124: R401 = R401::new(1.0, 23);
pub const e134: R401 = R401::new(1.0, 24);
pub const e234: R401 = R401::new(1.0, 25);
pub const e0123: R401 = R401::new(1.0, 26);
pub const e0124: R401 = R401::new(1.0, 27);
pub const e0134: R401 = R401::new(1.0, 28);
pub const e0234: R401 = R401::new(1.0, 29);
pub const e1234: R401 = R401::new(1.0, 30);
pub const e01234: R401 = R401::new(1.0, 31);
impl Index<usize> for R401 {
type Output = float_t;
fn index<'a>(&'a self, index: usize) -> &'a Self::Output {
&self.mvec[index]
}
}
impl IndexMut<usize> for R401 {
fn index_mut<'a>(&'a mut self, index: usize) -> &'a mut Self::Output {
&mut self.mvec[index]
}
}
impl fmt::Display for R401 {
fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result {
let mut n = 0;
let ret = self.mvec.iter().enumerate().filter_map(|(i, &coeff)| {
if coeff > 0.00001 || coeff < -0.00001 {
n = 1;
Some(format!("{}{}",
format!("{:.*}", 7, coeff).trim_end_matches('0').trim_end_matches('.'),
if i > 0 { basis[i] } else { "" }
)
)
} else {
None
}
}).collect::<Vec<String>>().join(" + ");
if n==0 { write!(f,"0") } else { write!(f, "{}", ret) }
}
}
impl From<float_t> for R401 {
fn from(value: float_t) -> Self {
R401::new(value, 0)
}
}
impl From<R401> for float_t {
fn from(value: R401) -> Self {
value[0]
}
}
// Reverse
// Reverse the order of the basis blades.
impl R401 {
pub fn reverse(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[0];
res[1]=a[1];
res[2]=a[2];
res[3]=a[3];
res[4]=a[4];
res[5]=a[5];
res[6]=-a[6];
res[7]=-a[7];
res[8]=-a[8];
res[9]=-a[9];
res[10]=-a[10];
res[11]=-a[11];
res[12]=-a[12];
res[13]=-a[13];
res[14]=-a[14];
res[15]=-a[15];
res[16]=-a[16];
res[17]=-a[17];
res[18]=-a[18];
res[19]=-a[19];
res[20]=-a[20];
res[21]=-a[21];
res[22]=-a[22];
res[23]=-a[23];
res[24]=-a[24];
res[25]=-a[25];
res[26]=a[26];
res[27]=a[27];
res[28]=a[28];
res[29]=a[29];
res[30]=a[30];
res[31]=a[31];
res
}
}
// Dual
// Poincare duality operator.
impl R401 {
pub fn dual(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[31];
res[1]=a[30];
res[2]=a[29];
res[3]=a[28];
res[4]=a[27];
res[5]=a[26];
res[6]=a[25];
res[7]=a[24];
res[8]=a[23];
res[9]=a[22];
res[10]=a[21];
res[11]=a[20];
res[12]=a[19];
res[13]=a[18];
res[14]=a[17];
res[15]=a[16];
res[16]=a[15];
res[17]=a[14];
res[18]=a[13];
res[19]=a[12];
res[20]=a[11];
res[21]=a[10];
res[22]=a[9];
res[23]=a[8];
res[24]=a[7];
res[25]=a[6];
res[26]=a[5];
res[27]=a[4];
res[28]=a[3];
res[29]=a[2];
res[30]=a[1];
res[31]=a[0];
res
}
}
// Hodge star
impl R401 {
pub fn dual_h(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[31];
res[1]=a[30];
res[2]=-a[29];
res[3]=a[28];
res[4]=-a[27];
res[5]=a[26];
res[6]=a[25];
res[7]=-a[24];
res[8]=a[23];
res[9]=-a[22];
res[10]=a[21];
res[11]=-a[20];
res[12]=a[19];
res[13]=a[18];
res[14]=-a[17];
res[15]=a[16];
res[16]=a[15];
res[17]=-a[14];
res[18]=a[13];
res[19]=a[12];
res[20]=-a[11];
res[21]=a[10];
res[22]=-a[9];
res[23]=a[8];
res[24]=-a[7];
res[25]=a[6];
res[26]=a[5];
res[27]=-a[4];
res[28]=a[3];
res[29]=-a[2];
res[30]=a[1];
res[31]=a[0];
res
}
pub fn undual_h(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[31];
res[1]=a[30];
res[2]=-a[29];
res[3]=a[28];
res[4]=-a[27];
res[5]=a[26];
res[6]=a[25];
res[7]=-a[24];
res[8]=a[23];
res[9]=-a[22];
res[10]=a[21];
res[11]=-a[20];
res[12]=a[19];
res[13]=a[18];
res[14]=-a[17];
res[15]=a[16];
res[16]=a[15];
res[17]=-a[14];
res[18]=a[13];
res[19]=a[12];
res[20]=-a[11];
res[21]=a[10];
res[22]=-a[9];
res[23]=a[8];
res[24]=-a[7];
res[25]=a[6];
res[26]=a[5];
res[27]=-a[4];
res[28]=a[3];
res[29]=-a[2];
res[30]=a[1];
res[31]=a[0];
res
}
}
impl Neg for R401 {
type Output = Self;
fn neg(self) -> Self::Output {
-1.0 * self
}
}
impl Not for R401 {
type Output = R401;
fn not(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[31];
res[1]=a[30];
res[2]=a[29];
res[3]=a[28];
res[4]=a[27];
res[5]=a[26];
res[6]=a[25];
res[7]=a[24];
res[8]=a[23];
res[9]=a[22];
res[10]=a[21];
res[11]=a[20];
res[12]=a[19];
res[13]=a[18];
res[14]=a[17];
res[15]=a[16];
res[16]=a[15];
res[17]=a[14];
res[18]=a[13];
res[19]=a[12];
res[20]=a[11];
res[21]=a[10];
res[22]=a[9];
res[23]=a[8];
res[24]=a[7];
res[25]=a[6];
res[26]=a[5];
res[27]=a[4];
res[28]=a[3];
res[29]=a[2];
res[30]=a[1];
res[31]=a[0];
res
}
}
// Conjugate
// Clifford Conjugation
impl R401 {
pub fn conjugate(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[0];
res[1]=-a[1];
res[2]=-a[2];
res[3]=-a[3];
res[4]=-a[4];
res[5]=-a[5];
res[6]=-a[6];
res[7]=-a[7];
res[8]=-a[8];
res[9]=-a[9];
res[10]=-a[10];
res[11]=-a[11];
res[12]=-a[12];
res[13]=-a[13];
res[14]=-a[14];
res[15]=-a[15];
res[16]=a[16];
res[17]=a[17];
res[18]=a[18];
res[19]=a[19];
res[20]=a[20];
res[21]=a[21];
res[22]=a[22];
res[23]=a[23];
res[24]=a[24];
res[25]=a[25];
res[26]=a[26];
res[27]=a[27];
res[28]=a[28];
res[29]=a[29];
res[30]=a[30];
res[31]=-a[31];
res
}
}
// Involute
// Main involution
impl R401 {
pub fn involute(self: Self) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=a[0];
res[1]=-a[1];
res[2]=-a[2];
res[3]=-a[3];
res[4]=-a[4];
res[5]=-a[5];
res[6]=a[6];
res[7]=a[7];
res[8]=a[8];
res[9]=a[9];
res[10]=a[10];
res[11]=a[11];
res[12]=a[12];
res[13]=a[13];
res[14]=a[14];
res[15]=a[15];
res[16]=-a[16];
res[17]=-a[17];
res[18]=-a[18];
res[19]=-a[19];
res[20]=-a[20];
res[21]=-a[21];
res[22]=-a[22];
res[23]=-a[23];
res[24]=-a[24];
res[25]=-a[25];
res[26]=a[26];
res[27]=a[27];
res[28]=a[28];
res[29]=a[29];
res[30]=a[30];
res[31]=-a[31];
res
}
}
// Mul
// The geometric product.
impl Mul for R401 {
type Output = R401;
fn mul(self: R401, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=b[0]*a[0]+b[2]*a[2]+b[3]*a[3]+b[4]*a[4]+b[5]*a[5]-b[10]*a[10]-b[11]*a[11]-b[12]*a[12]-b[13]*a[13]-b[14]*a[14]-b[15]*a[15]-b[22]*a[22]-b[23]*a[23]-b[24]*a[24]-b[25]*a[25]+b[30]*a[30];
res[1]=b[1]*a[0]+b[0]*a[1]-b[6]*a[2]-b[7]*a[3]-b[8]*a[4]-b[9]*a[5]+b[2]*a[6]+b[3]*a[7]+b[4]*a[8]+b[5]*a[9]-b[16]*a[10]-b[17]*a[11]-b[18]*a[12]-b[19]*a[13]-b[20]*a[14]-b[21]*a[15]-b[10]*a[16]-b[11]*a[17]-b[12]*a[18]-b[13]*a[19]-b[14]*a[20]-b[15]*a[21]+b[26]*a[22]+b[27]*a[23]+b[28]*a[24]+b[29]*a[25]-b[22]*a[26]-b[23]*a[27]-b[24]*a[28]-b[25]*a[29]+b[31]*a[30]+b[30]*a[31];
res[2]=b[2]*a[0]+b[0]*a[2]-b[10]*a[3]-b[11]*a[4]-b[12]*a[5]+b[3]*a[10]+b[4]*a[11]+b[5]*a[12]-b[22]*a[13]-b[23]*a[14]-b[24]*a[15]-b[13]*a[22]-b[14]*a[23]-b[15]*a[24]+b[30]*a[25]-b[25]*a[30];
res[3]=b[3]*a[0]+b[10]*a[2]+b[0]*a[3]-b[13]*a[4]-b[14]*a[5]-b[2]*a[10]+b[22]*a[11]+b[23]*a[12]+b[4]*a[13]+b[5]*a[14]-b[25]*a[15]+b[11]*a[22]+b[12]*a[23]-b[30]*a[24]-b[15]*a[25]+b[24]*a[30];
res[4]=b[4]*a[0]+b[11]*a[2]+b[13]*a[3]+b[0]*a[4]-b[15]*a[5]-b[22]*a[10]-b[2]*a[11]+b[24]*a[12]-b[3]*a[13]+b[25]*a[14]+b[5]*a[15]-b[10]*a[22]+b[30]*a[23]+b[12]*a[24]+b[14]*a[25]-b[23]*a[30];
res[5]=b[5]*a[0]+b[12]*a[2]+b[14]*a[3]+b[15]*a[4]+b[0]*a[5]-b[23]*a[10]-b[24]*a[11]-b[2]*a[12]-b[25]*a[13]-b[3]*a[14]-b[4]*a[15]-b[30]*a[22]-b[10]*a[23]-b[11]*a[24]-b[13]*a[25]+b[22]*a[30];
res[6]=b[6]*a[0]+b[2]*a[1]-b[1]*a[2]+b[16]*a[3]+b[17]*a[4]+b[18]*a[5]+b[0]*a[6]-b[10]*a[7]-b[11]*a[8]-b[12]*a[9]+b[7]*a[10]+b[8]*a[11]+b[9]*a[12]-b[26]*a[13]-b[27]*a[14]-b[28]*a[15]+b[3]*a[16]+b[4]*a[17]+b[5]*a[18]-b[22]*a[19]-b[23]*a[20]-b[24]*a[21]+b[19]*a[22]+b[20]*a[23]+b[21]*a[24]-b[31]*a[25]-b[13]*a[26]-b[14]*a[27]-b[15]*a[28]+b[30]*a[29]-b[29]*a[30]-b[25]*a[31];
res[7]=b[7]*a[0]+b[3]*a[1]-b[16]*a[2]-b[1]*a[3]+b[19]*a[4]+b[20]*a[5]+b[10]*a[6]+b[0]*a[7]-b[13]*a[8]-b[14]*a[9]-b[6]*a[10]+b[26]*a[11]+b[27]*a[12]+b[8]*a[13]+b[9]*a[14]-b[29]*a[15]-b[2]*a[16]+b[22]*a[17]+b[23]*a[18]+b[4]*a[19]+b[5]*a[20]-b[25]*a[21]-b[17]*a[22]-b[18]*a[23]+b[31]*a[24]+b[21]*a[25]+b[11]*a[26]+b[12]*a[27]-b[30]*a[28]-b[15]*a[29]+b[28]*a[30]+b[24]*a[31];
res[8]=b[8]*a[0]+b[4]*a[1]-b[17]*a[2]-b[19]*a[3]-b[1]*a[4]+b[21]*a[5]+b[11]*a[6]+b[13]*a[7]+b[0]*a[8]-b[15]*a[9]-b[26]*a[10]-b[6]*a[11]+b[28]*a[12]-b[7]*a[13]+b[29]*a[14]+b[9]*a[15]-b[22]*a[16]-b[2]*a[17]+b[24]*a[18]-b[3]*a[19]+b[25]*a[20]+b[5]*a[21]+b[16]*a[22]-b[31]*a[23]-b[18]*a[24]-b[20]*a[25]-b[10]*a[26]+b[30]*a[27]+b[12]*a[28]+b[14]*a[29]-b[27]*a[30]-b[23]*a[31];
res[9]=b[9]*a[0]+b[5]*a[1]-b[18]*a[2]-b[20]*a[3]-b[21]*a[4]-b[1]*a[5]+b[12]*a[6]+b[14]*a[7]+b[15]*a[8]+b[0]*a[9]-b[27]*a[10]-b[28]*a[11]-b[6]*a[12]-b[29]*a[13]-b[7]*a[14]-b[8]*a[15]-b[23]*a[16]-b[24]*a[17]-b[2]*a[18]-b[25]*a[19]-b[3]*a[20]-b[4]*a[21]+b[31]*a[22]+b[16]*a[23]+b[17]*a[24]+b[19]*a[25]-b[30]*a[26]-b[10]*a[27]-b[11]*a[28]-b[13]*a[29]+b[26]*a[30]+b[22]*a[31];
res[10]=b[10]*a[0]+b[3]*a[2]-b[2]*a[3]+b[22]*a[4]+b[23]*a[5]+b[0]*a[10]-b[13]*a[11]-b[14]*a[12]+b[11]*a[13]+b[12]*a[14]-b[30]*a[15]+b[4]*a[22]+b[5]*a[23]-b[25]*a[24]+b[24]*a[25]-b[15]*a[30];
res[11]=b[11]*a[0]+b[4]*a[2]-b[22]*a[3]-b[2]*a[4]+b[24]*a[5]+b[13]*a[10]+b[0]*a[11]-b[15]*a[12]-b[10]*a[13]+b[30]*a[14]+b[12]*a[15]-b[3]*a[22]+b[25]*a[23]+b[5]*a[24]-b[23]*a[25]+b[14]*a[30];
res[12]=b[12]*a[0]+b[5]*a[2]-b[23]*a[3]-b[24]*a[4]-b[2]*a[5]+b[14]*a[10]+b[15]*a[11]+b[0]*a[12]-b[30]*a[13]-b[10]*a[14]-b[11]*a[15]-b[25]*a[22]-b[3]*a[23]-b[4]*a[24]+b[22]*a[25]-b[13]*a[30];
res[13]=b[13]*a[0]+b[22]*a[2]+b[4]*a[3]-b[3]*a[4]+b[25]*a[5]-b[11]*a[10]+b[10]*a[11]-b[30]*a[12]+b[0]*a[13]-b[15]*a[14]+b[14]*a[15]+b[2]*a[22]-b[24]*a[23]+b[23]*a[24]+b[5]*a[25]-b[12]*a[30];
res[14]=b[14]*a[0]+b[23]*a[2]+b[5]*a[3]-b[25]*a[4]-b[3]*a[5]-b[12]*a[10]+b[30]*a[11]+b[10]*a[12]+b[15]*a[13]+b[0]*a[14]-b[13]*a[15]+b[24]*a[22]+b[2]*a[23]-b[22]*a[24]-b[4]*a[25]+b[11]*a[30];
res[15]=b[15]*a[0]+b[24]*a[2]+b[25]*a[3]+b[5]*a[4]-b[4]*a[5]-b[30]*a[10]-b[12]*a[11]+b[11]*a[12]-b[14]*a[13]+b[13]*a[14]+b[0]*a[15]-b[23]*a[22]+b[22]*a[23]+b[2]*a[24]+b[3]*a[25]-b[10]*a[30];
res[16]=b[16]*a[0]+b[10]*a[1]-b[7]*a[2]+b[6]*a[3]-b[26]*a[4]-b[27]*a[5]+b[3]*a[6]-b[2]*a[7]+b[22]*a[8]+b[23]*a[9]+b[1]*a[10]-b[19]*a[11]-b[20]*a[12]+b[17]*a[13]+b[18]*a[14]-b[31]*a[15]+b[0]*a[16]-b[13]*a[17]-b[14]*a[18]+b[11]*a[19]+b[12]*a[20]-b[30]*a[21]-b[8]*a[22]-b[9]*a[23]+b[29]*a[24]-b[28]*a[25]+b[4]*a[26]+b[5]*a[27]-b[25]*a[28]+b[24]*a[29]-b[21]*a[30]-b[15]*a[31];
res[17]=b[17]*a[0]+b[11]*a[1]-b[8]*a[2]+b[26]*a[3]+b[6]*a[4]-b[28]*a[5]+b[4]*a[6]-b[22]*a[7]-b[2]*a[8]+b[24]*a[9]+b[19]*a[10]+b[1]*a[11]-b[21]*a[12]-b[16]*a[13]+b[31]*a[14]+b[18]*a[15]+b[13]*a[16]+b[0]*a[17]-b[15]*a[18]-b[10]*a[19]+b[30]*a[20]+b[12]*a[21]+b[7]*a[22]-b[29]*a[23]-b[9]*a[24]+b[27]*a[25]-b[3]*a[26]+b[25]*a[27]+b[5]*a[28]-b[23]*a[29]+b[20]*a[30]+b[14]*a[31];
res[18]=b[18]*a[0]+b[12]*a[1]-b[9]*a[2]+b[27]*a[3]+b[28]*a[4]+b[6]*a[5]+b[5]*a[6]-b[23]*a[7]-b[24]*a[8]-b[2]*a[9]+b[20]*a[10]+b[21]*a[11]+b[1]*a[12]-b[31]*a[13]-b[16]*a[14]-b[17]*a[15]+b[14]*a[16]+b[15]*a[17]+b[0]*a[18]-b[30]*a[19]-b[10]*a[20]-b[11]*a[21]+b[29]*a[22]+b[7]*a[23]+b[8]*a[24]-b[26]*a[25]-b[25]*a[26]-b[3]*a[27]-b[4]*a[28]+b[22]*a[29]-b[19]*a[30]-b[13]*a[31];
res[19]=b[19]*a[0]+b[13]*a[1]-b[26]*a[2]-b[8]*a[3]+b[7]*a[4]-b[29]*a[5]+b[22]*a[6]+b[4]*a[7]-b[3]*a[8]+b[25]*a[9]-b[17]*a[10]+b[16]*a[11]-b[31]*a[12]+b[1]*a[13]-b[21]*a[14]+b[20]*a[15]-b[11]*a[16]+b[10]*a[17]-b[30]*a[18]+b[0]*a[19]-b[15]*a[20]+b[14]*a[21]-b[6]*a[22]+b[28]*a[23]-b[27]*a[24]-b[9]*a[25]+b[2]*a[26]-b[24]*a[27]+b[23]*a[28]+b[5]*a[29]-b[18]*a[30]-b[12]*a[31];
res[20]=b[20]*a[0]+b[14]*a[1]-b[27]*a[2]-b[9]*a[3]+b[29]*a[4]+b[7]*a[5]+b[23]*a[6]+b[5]*a[7]-b[25]*a[8]-b[3]*a[9]-b[18]*a[10]+b[31]*a[11]+b[16]*a[12]+b[21]*a[13]+b[1]*a[14]-b[19]*a[15]-b[12]*a[16]+b[30]*a[17]+b[10]*a[18]+b[15]*a[19]+b[0]*a[20]-b[13]*a[21]-b[28]*a[22]-b[6]*a[23]+b[26]*a[24]+b[8]*a[25]+b[24]*a[26]+b[2]*a[27]-b[22]*a[28]-b[4]*a[29]+b[17]*a[30]+b[11]*a[31];
res[21]=b[21]*a[0]+b[15]*a[1]-b[28]*a[2]-b[29]*a[3]-b[9]*a[4]+b[8]*a[5]+b[24]*a[6]+b[25]*a[7]+b[5]*a[8]-b[4]*a[9]-b[31]*a[10]-b[18]*a[11]+b[17]*a[12]-b[20]*a[13]+b[19]*a[14]+b[1]*a[15]-b[30]*a[16]-b[12]*a[17]+b[11]*a[18]-b[14]*a[19]+b[13]*a[20]+b[0]*a[21]+b[27]*a[22]-b[26]*a[23]-b[6]*a[24]-b[7]*a[25]-b[23]*a[26]+b[22]*a[27]+b[2]*a[28]+b[3]*a[29]-b[16]*a[30]-b[10]*a[31];
res[22]=b[22]*a[0]+b[13]*a[2]-b[11]*a[3]+b[10]*a[4]-b[30]*a[5]+b[4]*a[10]-b[3]*a[11]+b[25]*a[12]+b[2]*a[13]-b[24]*a[14]+b[23]*a[15]+b[0]*a[22]-b[15]*a[23]+b[14]*a[24]-b[12]*a[25]+b[5]*a[30];
res[23]=b[23]*a[0]+b[14]*a[2]-b[12]*a[3]+b[30]*a[4]+b[10]*a[5]+b[5]*a[10]-b[25]*a[11]-b[3]*a[12]+b[24]*a[13]+b[2]*a[14]-b[22]*a[15]+b[15]*a[22]+b[0]*a[23]-b[13]*a[24]+b[11]*a[25]-b[4]*a[30];
res[24]=b[24]*a[0]+b[15]*a[2]-b[30]*a[3]-b[12]*a[4]+b[11]*a[5]+b[25]*a[10]+b[5]*a[11]-b[4]*a[12]-b[23]*a[13]+b[22]*a[14]+b[2]*a[15]-b[14]*a[22]+b[13]*a[23]+b[0]*a[24]-b[10]*a[25]+b[3]*a[30];
res[25]=b[25]*a[0]+b[30]*a[2]+b[15]*a[3]-b[14]*a[4]+b[13]*a[5]-b[24]*a[10]+b[23]*a[11]-b[22]*a[12]+b[5]*a[13]-b[4]*a[14]+b[3]*a[15]+b[12]*a[22]-b[11]*a[23]+b[10]*a[24]+b[0]*a[25]-b[2]*a[30];
res[26]=b[26]*a[0]+b[22]*a[1]-b[19]*a[2]+b[17]*a[3]-b[16]*a[4]+b[31]*a[5]+b[13]*a[6]-b[11]*a[7]+b[10]*a[8]-b[30]*a[9]+b[8]*a[10]-b[7]*a[11]+b[29]*a[12]+b[6]*a[13]-b[28]*a[14]+b[27]*a[15]+b[4]*a[16]-b[3]*a[17]+b[25]*a[18]+b[2]*a[19]-b[24]*a[20]+b[23]*a[21]-b[1]*a[22]+b[21]*a[23]-b[20]*a[24]+b[18]*a[25]+b[0]*a[26]-b[15]*a[27]+b[14]*a[28]-b[12]*a[29]+b[9]*a[30]+b[5]*a[31];
res[27]=b[27]*a[0]+b[23]*a[1]-b[20]*a[2]+b[18]*a[3]-b[31]*a[4]-b[16]*a[5]+b[14]*a[6]-b[12]*a[7]+b[30]*a[8]+b[10]*a[9]+b[9]*a[10]-b[29]*a[11]-b[7]*a[12]+b[28]*a[13]+b[6]*a[14]-b[26]*a[15]+b[5]*a[16]-b[25]*a[17]-b[3]*a[18]+b[24]*a[19]+b[2]*a[20]-b[22]*a[21]-b[21]*a[22]-b[1]*a[23]+b[19]*a[24]-b[17]*a[25]+b[15]*a[26]+b[0]*a[27]-b[13]*a[28]+b[11]*a[29]-b[8]*a[30]-b[4]*a[31];
res[28]=b[28]*a[0]+b[24]*a[1]-b[21]*a[2]+b[31]*a[3]+b[18]*a[4]-b[17]*a[5]+b[15]*a[6]-b[30]*a[7]-b[12]*a[8]+b[11]*a[9]+b[29]*a[10]+b[9]*a[11]-b[8]*a[12]-b[27]*a[13]+b[26]*a[14]+b[6]*a[15]+b[25]*a[16]+b[5]*a[17]-b[4]*a[18]-b[23]*a[19]+b[22]*a[20]+b[2]*a[21]+b[20]*a[22]-b[19]*a[23]-b[1]*a[24]+b[16]*a[25]-b[14]*a[26]+b[13]*a[27]+b[0]*a[28]-b[10]*a[29]+b[7]*a[30]+b[3]*a[31];
res[29]=b[29]*a[0]+b[25]*a[1]-b[31]*a[2]-b[21]*a[3]+b[20]*a[4]-b[19]*a[5]+b[30]*a[6]+b[15]*a[7]-b[14]*a[8]+b[13]*a[9]-b[28]*a[10]+b[27]*a[11]-b[26]*a[12]+b[9]*a[13]-b[8]*a[14]+b[7]*a[15]-b[24]*a[16]+b[23]*a[17]-b[22]*a[18]+b[5]*a[19]-b[4]*a[20]+b[3]*a[21]-b[18]*a[22]+b[17]*a[23]-b[16]*a[24]-b[1]*a[25]+b[12]*a[26]-b[11]*a[27]+b[10]*a[28]+b[0]*a[29]-b[6]*a[30]-b[2]*a[31];
res[30]=b[30]*a[0]+b[25]*a[2]-b[24]*a[3]+b[23]*a[4]-b[22]*a[5]+b[15]*a[10]-b[14]*a[11]+b[13]*a[12]+b[12]*a[13]-b[11]*a[14]+b[10]*a[15]+b[5]*a[22]-b[4]*a[23]+b[3]*a[24]-b[2]*a[25]+b[0]*a[30];
res[31]=b[31]*a[0]+b[30]*a[1]-b[29]*a[2]+b[28]*a[3]-b[27]*a[4]+b[26]*a[5]+b[25]*a[6]-b[24]*a[7]+b[23]*a[8]-b[22]*a[9]+b[21]*a[10]-b[20]*a[11]+b[19]*a[12]+b[18]*a[13]-b[17]*a[14]+b[16]*a[15]+b[15]*a[16]-b[14]*a[17]+b[13]*a[18]+b[12]*a[19]-b[11]*a[20]+b[10]*a[21]-b[9]*a[22]+b[8]*a[23]-b[7]*a[24]+b[6]*a[25]+b[5]*a[26]-b[4]*a[27]+b[3]*a[28]-b[2]*a[29]+b[1]*a[30]+b[0]*a[31];
res
}
}
// Wedge
// The outer product. (MEET)
impl BitXor for R401 {
type Output = R401;
fn bitxor(self: R401, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=b[0]*a[0];
res[1]=b[1]*a[0]+b[0]*a[1];
res[2]=b[2]*a[0]+b[0]*a[2];
res[3]=b[3]*a[0]+b[0]*a[3];
res[4]=b[4]*a[0]+b[0]*a[4];
res[5]=b[5]*a[0]+b[0]*a[5];
res[6]=b[6]*a[0]+b[2]*a[1]-b[1]*a[2]+b[0]*a[6];
res[7]=b[7]*a[0]+b[3]*a[1]-b[1]*a[3]+b[0]*a[7];
res[8]=b[8]*a[0]+b[4]*a[1]-b[1]*a[4]+b[0]*a[8];
res[9]=b[9]*a[0]+b[5]*a[1]-b[1]*a[5]+b[0]*a[9];
res[10]=b[10]*a[0]+b[3]*a[2]-b[2]*a[3]+b[0]*a[10];
res[11]=b[11]*a[0]+b[4]*a[2]-b[2]*a[4]+b[0]*a[11];
res[12]=b[12]*a[0]+b[5]*a[2]-b[2]*a[5]+b[0]*a[12];
res[13]=b[13]*a[0]+b[4]*a[3]-b[3]*a[4]+b[0]*a[13];
res[14]=b[14]*a[0]+b[5]*a[3]-b[3]*a[5]+b[0]*a[14];
res[15]=b[15]*a[0]+b[5]*a[4]-b[4]*a[5]+b[0]*a[15];
res[16]=b[16]*a[0]+b[10]*a[1]-b[7]*a[2]+b[6]*a[3]+b[3]*a[6]-b[2]*a[7]+b[1]*a[10]+b[0]*a[16];
res[17]=b[17]*a[0]+b[11]*a[1]-b[8]*a[2]+b[6]*a[4]+b[4]*a[6]-b[2]*a[8]+b[1]*a[11]+b[0]*a[17];
res[18]=b[18]*a[0]+b[12]*a[1]-b[9]*a[2]+b[6]*a[5]+b[5]*a[6]-b[2]*a[9]+b[1]*a[12]+b[0]*a[18];
res[19]=b[19]*a[0]+b[13]*a[1]-b[8]*a[3]+b[7]*a[4]+b[4]*a[7]-b[3]*a[8]+b[1]*a[13]+b[0]*a[19];
res[20]=b[20]*a[0]+b[14]*a[1]-b[9]*a[3]+b[7]*a[5]+b[5]*a[7]-b[3]*a[9]+b[1]*a[14]+b[0]*a[20];
res[21]=b[21]*a[0]+b[15]*a[1]-b[9]*a[4]+b[8]*a[5]+b[5]*a[8]-b[4]*a[9]+b[1]*a[15]+b[0]*a[21];
res[22]=b[22]*a[0]+b[13]*a[2]-b[11]*a[3]+b[10]*a[4]+b[4]*a[10]-b[3]*a[11]+b[2]*a[13]+b[0]*a[22];
res[23]=b[23]*a[0]+b[14]*a[2]-b[12]*a[3]+b[10]*a[5]+b[5]*a[10]-b[3]*a[12]+b[2]*a[14]+b[0]*a[23];
res[24]=b[24]*a[0]+b[15]*a[2]-b[12]*a[4]+b[11]*a[5]+b[5]*a[11]-b[4]*a[12]+b[2]*a[15]+b[0]*a[24];
res[25]=b[25]*a[0]+b[15]*a[3]-b[14]*a[4]+b[13]*a[5]+b[5]*a[13]-b[4]*a[14]+b[3]*a[15]+b[0]*a[25];
res[26]=b[26]*a[0]+b[22]*a[1]-b[19]*a[2]+b[17]*a[3]-b[16]*a[4]+b[13]*a[6]-b[11]*a[7]+b[10]*a[8]+b[8]*a[10]-b[7]*a[11]+b[6]*a[13]+b[4]*a[16]-b[3]*a[17]+b[2]*a[19]-b[1]*a[22]+b[0]*a[26];
res[27]=b[27]*a[0]+b[23]*a[1]-b[20]*a[2]+b[18]*a[3]-b[16]*a[5]+b[14]*a[6]-b[12]*a[7]+b[10]*a[9]+b[9]*a[10]-b[7]*a[12]+b[6]*a[14]+b[5]*a[16]-b[3]*a[18]+b[2]*a[20]-b[1]*a[23]+b[0]*a[27];
res[28]=b[28]*a[0]+b[24]*a[1]-b[21]*a[2]+b[18]*a[4]-b[17]*a[5]+b[15]*a[6]-b[12]*a[8]+b[11]*a[9]+b[9]*a[11]-b[8]*a[12]+b[6]*a[15]+b[5]*a[17]-b[4]*a[18]+b[2]*a[21]-b[1]*a[24]+b[0]*a[28];
res[29]=b[29]*a[0]+b[25]*a[1]-b[21]*a[3]+b[20]*a[4]-b[19]*a[5]+b[15]*a[7]-b[14]*a[8]+b[13]*a[9]+b[9]*a[13]-b[8]*a[14]+b[7]*a[15]+b[5]*a[19]-b[4]*a[20]+b[3]*a[21]-b[1]*a[25]+b[0]*a[29];
res[30]=b[30]*a[0]+b[25]*a[2]-b[24]*a[3]+b[23]*a[4]-b[22]*a[5]+b[15]*a[10]-b[14]*a[11]+b[13]*a[12]+b[12]*a[13]-b[11]*a[14]+b[10]*a[15]+b[5]*a[22]-b[4]*a[23]+b[3]*a[24]-b[2]*a[25]+b[0]*a[30];
res[31]=b[31]*a[0]+b[30]*a[1]-b[29]*a[2]+b[28]*a[3]-b[27]*a[4]+b[26]*a[5]+b[25]*a[6]-b[24]*a[7]+b[23]*a[8]-b[22]*a[9]+b[21]*a[10]-b[20]*a[11]+b[19]*a[12]+b[18]*a[13]-b[17]*a[14]+b[16]*a[15]+b[15]*a[16]-b[14]*a[17]+b[13]*a[18]+b[12]*a[19]-b[11]*a[20]+b[10]*a[21]-b[9]*a[22]+b[8]*a[23]-b[7]*a[24]+b[6]*a[25]+b[5]*a[26]-b[4]*a[27]+b[3]*a[28]-b[2]*a[29]+b[1]*a[30]+b[0]*a[31];
res
}
}
// Vee
// The regressive product. (JOIN)
impl BitAnd for R401 {
type Output = R401;
fn bitand(self: R401, b: R401) -> R401 {
// return (self.dual_h() ^ b.dual_h()).undual_h();
let mut res = R401::zero();
let a = self;
res[31]=1.0*(a[31]*b[31]);
res[30]=1.0*(a[30]*b[31]+a[31]*b[30]);
res[29]=-1.0*(a[29]*-1.0*b[31]+a[31]*b[29]*-1.0);
res[28]=1.0*(a[28]*b[31]+a[31]*b[28]);
res[27]=-1.0*(a[27]*-1.0*b[31]+a[31]*b[27]*-1.0);
res[26]=1.0*(a[26]*b[31]+a[31]*b[26]);
res[25]=1.0*(a[25]*b[31]+a[29]*-1.0*b[30]-a[30]*b[29]*-1.0+a[31]*b[25]);
res[24]=-1.0*(a[24]*-1.0*b[31]+a[28]*b[30]-a[30]*b[28]+a[31]*b[24]*-1.0);
res[23]=1.0*(a[23]*b[31]+a[27]*-1.0*b[30]-a[30]*b[27]*-1.0+a[31]*b[23]);
res[22]=-1.0*(a[22]*-1.0*b[31]+a[26]*b[30]-a[30]*b[26]+a[31]*b[22]*-1.0);
res[21]=1.0*(a[21]*b[31]+a[28]*b[29]*-1.0-a[29]*-1.0*b[28]+a[31]*b[21]);
res[20]=-1.0*(a[20]*-1.0*b[31]+a[27]*-1.0*b[29]*-1.0-a[29]*-1.0*b[27]*-1.0+a[31]*b[20]*-1.0);
res[19]=1.0*(a[19]*b[31]+a[26]*b[29]*-1.0-a[29]*-1.0*b[26]+a[31]*b[19]);
res[18]=1.0*(a[18]*b[31]+a[27]*-1.0*b[28]-a[28]*b[27]*-1.0+a[31]*b[18]);
res[17]=-1.0*(a[17]*-1.0*b[31]+a[26]*b[28]-a[28]*b[26]+a[31]*b[17]*-1.0);
res[16]=1.0*(a[16]*b[31]+a[26]*b[27]*-1.0-a[27]*-1.0*b[26]+a[31]*b[16]);
res[15]=1.0*(a[15]*b[31]+a[21]*b[30]-a[24]*-1.0*b[29]*-1.0+a[25]*b[28]+a[28]*b[25]-a[29]*-1.0*b[24]*-1.0+a[30]*b[21]+a[31]*b[15]);
res[14]=-1.0*(a[14]*-1.0*b[31]+a[20]*-1.0*b[30]-a[23]*b[29]*-1.0+a[25]*b[27]*-1.0+a[27]*-1.0*b[25]-a[29]*-1.0*b[23]+a[30]*b[20]*-1.0+a[31]*b[14]*-1.0);
res[13]=1.0*(a[13]*b[31]+a[19]*b[30]-a[22]*-1.0*b[29]*-1.0+a[25]*b[26]+a[26]*b[25]-a[29]*-1.0*b[22]*-1.0+a[30]*b[19]+a[31]*b[13]);
res[12]=1.0*(a[12]*b[31]+a[18]*b[30]-a[23]*b[28]+a[24]*-1.0*b[27]*-1.0+a[27]*-1.0*b[24]*-1.0-a[28]*b[23]+a[30]*b[18]+a[31]*b[12]);
res[11]=-1.0*(a[11]*-1.0*b[31]+a[17]*-1.0*b[30]-a[22]*-1.0*b[28]+a[24]*-1.0*b[26]+a[26]*b[24]*-1.0-a[28]*b[22]*-1.0+a[30]*b[17]*-1.0+a[31]*b[11]*-1.0);
res[10]=1.0*(a[10]*b[31]+a[16]*b[30]-a[22]*-1.0*b[27]*-1.0+a[23]*b[26]+a[26]*b[23]-a[27]*-1.0*b[22]*-1.0+a[30]*b[16]+a[31]*b[10]);
res[9]=-1.0*(a[9]*-1.0*b[31]+a[18]*b[29]*-1.0-a[20]*-1.0*b[28]+a[21]*b[27]*-1.0+a[27]*-1.0*b[21]-a[28]*b[20]*-1.0+a[29]*-1.0*b[18]+a[31]*b[9]*-1.0);
res[8]=1.0*(a[8]*b[31]+a[17]*-1.0*b[29]*-1.0-a[19]*b[28]+a[21]*b[26]+a[26]*b[21]-a[28]*b[19]+a[29]*-1.0*b[17]*-1.0+a[31]*b[8]);
res[7]=-1.0*(a[7]*-1.0*b[31]+a[16]*b[29]*-1.0-a[19]*b[27]*-1.0+a[20]*-1.0*b[26]+a[26]*b[20]*-1.0-a[27]*-1.0*b[19]+a[29]*-1.0*b[16]+a[31]*b[7]*-1.0);
res[6]=1.0*(a[6]*b[31]+a[16]*b[28]-a[17]*-1.0*b[27]*-1.0+a[18]*b[26]+a[26]*b[18]-a[27]*-1.0*b[17]*-1.0+a[28]*b[16]+a[31]*b[6]);
res[5]=1.0*(a[5]*b[31]+a[9]*-1.0*b[30]-a[12]*b[29]*-1.0+a[14]*-1.0*b[28]-a[15]*b[27]*-1.0+a[18]*b[25]-a[20]*-1.0*b[24]*-1.0+a[21]*b[23]+a[23]*b[21]-a[24]*-1.0*b[20]*-1.0+a[25]*b[18]+a[27]*-1.0*b[15]-a[28]*b[14]*-1.0+a[29]*-1.0*b[12]-a[30]*b[9]*-1.0+a[31]*b[5]);
res[4]=-1.0*(a[4]*-1.0*b[31]+a[8]*b[30]-a[11]*-1.0*b[29]*-1.0+a[13]*b[28]-a[15]*b[26]+a[17]*-1.0*b[25]-a[19]*b[24]*-1.0+a[21]*b[22]*-1.0+a[22]*-1.0*b[21]-a[24]*-1.0*b[19]+a[25]*b[17]*-1.0+a[26]*b[15]-a[28]*b[13]+a[29]*-1.0*b[11]*-1.0-a[30]*b[8]+a[31]*b[4]*-1.0);
res[3]=1.0*(a[3]*b[31]+a[7]*-1.0*b[30]-a[10]*b[29]*-1.0+a[13]*b[27]*-1.0-a[14]*-1.0*b[26]+a[16]*b[25]-a[19]*b[23]+a[20]*-1.0*b[22]*-1.0+a[22]*-1.0*b[20]*-1.0-a[23]*b[19]+a[25]*b[16]+a[26]*b[14]*-1.0-a[27]*-1.0*b[13]+a[29]*-1.0*b[10]-a[30]*b[7]*-1.0+a[31]*b[3]);
res[2]=-1.0*(a[2]*-1.0*b[31]+a[6]*b[30]-a[10]*b[28]+a[11]*-1.0*b[27]*-1.0-a[12]*b[26]+a[16]*b[24]*-1.0-a[17]*-1.0*b[23]+a[18]*b[22]*-1.0+a[22]*-1.0*b[18]-a[23]*b[17]*-1.0+a[24]*-1.0*b[16]+a[26]*b[12]-a[27]*-1.0*b[11]*-1.0+a[28]*b[10]-a[30]*b[6]+a[31]*b[2]*-1.0);
res[1]=1.0*(a[1]*b[31]+a[6]*b[29]*-1.0-a[7]*-1.0*b[28]+a[8]*b[27]*-1.0-a[9]*-1.0*b[26]+a[16]*b[21]-a[17]*-1.0*b[20]*-1.0+a[18]*b[19]+a[19]*b[18]-a[20]*-1.0*b[17]*-1.0+a[21]*b[16]+a[26]*b[9]*-1.0-a[27]*-1.0*b[8]+a[28]*b[7]*-1.0-a[29]*-1.0*b[6]+a[31]*b[1]);
res[0]=1.0*(a[0]*b[31]+a[1]*b[30]-a[2]*-1.0*b[29]*-1.0+a[3]*b[28]-a[4]*-1.0*b[27]*-1.0+a[5]*b[26]+a[6]*b[25]-a[7]*-1.0*b[24]*-1.0+a[8]*b[23]-a[9]*-1.0*b[22]*-1.0+a[10]*b[21]-a[11]*-1.0*b[20]*-1.0+a[12]*b[19]+a[13]*b[18]-a[14]*-1.0*b[17]*-1.0+a[15]*b[16]+a[16]*b[15]-a[17]*-1.0*b[14]*-1.0+a[18]*b[13]+a[19]*b[12]-a[20]*-1.0*b[11]*-1.0+a[21]*b[10]-a[22]*-1.0*b[9]*-1.0+a[23]*b[8]-a[24]*-1.0*b[7]*-1.0+a[25]*b[6]+a[26]*b[5]-a[27]*-1.0*b[4]*-1.0+a[28]*b[3]-a[29]*-1.0*b[2]*-1.0+a[30]*b[1]+a[31]*b[0]);
res
}
}
// Dot
// The inner product.
impl BitOr for R401 {
type Output = R401;
fn bitor(self: R401, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0]=b[0]*a[0]+b[2]*a[2]+b[3]*a[3]+b[4]*a[4]+b[5]*a[5]-b[10]*a[10]-b[11]*a[11]-b[12]*a[12]-b[13]*a[13]-b[14]*a[14]-b[15]*a[15]-b[22]*a[22]-b[23]*a[23]-b[24]*a[24]-b[25]*a[25]+b[30]*a[30];
res[1]=b[1]*a[0]+b[0]*a[1]-b[6]*a[2]-b[7]*a[3]-b[8]*a[4]-b[9]*a[5]+b[2]*a[6]+b[3]*a[7]+b[4]*a[8]+b[5]*a[9]-b[16]*a[10]-b[17]*a[11]-b[18]*a[12]-b[19]*a[13]-b[20]*a[14]-b[21]*a[15]-b[10]*a[16]-b[11]*a[17]-b[12]*a[18]-b[13]*a[19]-b[14]*a[20]-b[15]*a[21]+b[26]*a[22]+b[27]*a[23]+b[28]*a[24]+b[29]*a[25]-b[22]*a[26]-b[23]*a[27]-b[24]*a[28]-b[25]*a[29]+b[31]*a[30]+b[30]*a[31];
res[2]=b[2]*a[0]+b[0]*a[2]-b[10]*a[3]-b[11]*a[4]-b[12]*a[5]+b[3]*a[10]+b[4]*a[11]+b[5]*a[12]-b[22]*a[13]-b[23]*a[14]-b[24]*a[15]-b[13]*a[22]-b[14]*a[23]-b[15]*a[24]+b[30]*a[25]-b[25]*a[30];
res[3]=b[3]*a[0]+b[10]*a[2]+b[0]*a[3]-b[13]*a[4]-b[14]*a[5]-b[2]*a[10]+b[22]*a[11]+b[23]*a[12]+b[4]*a[13]+b[5]*a[14]-b[25]*a[15]+b[11]*a[22]+b[12]*a[23]-b[30]*a[24]-b[15]*a[25]+b[24]*a[30];
res[4]=b[4]*a[0]+b[11]*a[2]+b[13]*a[3]+b[0]*a[4]-b[15]*a[5]-b[22]*a[10]-b[2]*a[11]+b[24]*a[12]-b[3]*a[13]+b[25]*a[14]+b[5]*a[15]-b[10]*a[22]+b[30]*a[23]+b[12]*a[24]+b[14]*a[25]-b[23]*a[30];
res[5]=b[5]*a[0]+b[12]*a[2]+b[14]*a[3]+b[15]*a[4]+b[0]*a[5]-b[23]*a[10]-b[24]*a[11]-b[2]*a[12]-b[25]*a[13]-b[3]*a[14]-b[4]*a[15]-b[30]*a[22]-b[10]*a[23]-b[11]*a[24]-b[13]*a[25]+b[22]*a[30];
res[6]=b[6]*a[0]+b[16]*a[3]+b[17]*a[4]+b[18]*a[5]+b[0]*a[6]-b[26]*a[13]-b[27]*a[14]-b[28]*a[15]+b[3]*a[16]+b[4]*a[17]+b[5]*a[18]-b[31]*a[25]-b[13]*a[26]-b[14]*a[27]-b[15]*a[28]-b[25]*a[31];
res[7]=b[7]*a[0]-b[16]*a[2]+b[19]*a[4]+b[20]*a[5]+b[0]*a[7]+b[26]*a[11]+b[27]*a[12]-b[29]*a[15]-b[2]*a[16]+b[4]*a[19]+b[5]*a[20]+b[31]*a[24]+b[11]*a[26]+b[12]*a[27]-b[15]*a[29]+b[24]*a[31];
res[8]=b[8]*a[0]-b[17]*a[2]-b[19]*a[3]+b[21]*a[5]+b[0]*a[8]-b[26]*a[10]+b[28]*a[12]+b[29]*a[14]-b[2]*a[17]-b[3]*a[19]+b[5]*a[21]-b[31]*a[23]-b[10]*a[26]+b[12]*a[28]+b[14]*a[29]-b[23]*a[31];
res[9]=b[9]*a[0]-b[18]*a[2]-b[20]*a[3]-b[21]*a[4]+b[0]*a[9]-b[27]*a[10]-b[28]*a[11]-b[29]*a[13]-b[2]*a[18]-b[3]*a[20]-b[4]*a[21]+b[31]*a[22]-b[10]*a[27]-b[11]*a[28]-b[13]*a[29]+b[22]*a[31];
res[10]=b[10]*a[0]+b[22]*a[4]+b[23]*a[5]+b[0]*a[10]-b[30]*a[15]+b[4]*a[22]+b[5]*a[23]-b[15]*a[30];
res[11]=b[11]*a[0]-b[22]*a[3]+b[24]*a[5]+b[0]*a[11]+b[30]*a[14]-b[3]*a[22]+b[5]*a[24]+b[14]*a[30];
res[12]=b[12]*a[0]-b[23]*a[3]-b[24]*a[4]+b[0]*a[12]-b[30]*a[13]-b[3]*a[23]-b[4]*a[24]-b[13]*a[30];
res[13]=b[13]*a[0]+b[22]*a[2]+b[25]*a[5]-b[30]*a[12]+b[0]*a[13]+b[2]*a[22]+b[5]*a[25]-b[12]*a[30];
res[14]=b[14]*a[0]+b[23]*a[2]-b[25]*a[4]+b[30]*a[11]+b[0]*a[14]+b[2]*a[23]-b[4]*a[25]+b[11]*a[30];
res[15]=b[15]*a[0]+b[24]*a[2]+b[25]*a[3]-b[30]*a[10]+b[0]*a[15]+b[2]*a[24]+b[3]*a[25]-b[10]*a[30];
res[16]=b[16]*a[0]-b[26]*a[4]-b[27]*a[5]-b[31]*a[15]+b[0]*a[16]+b[4]*a[26]+b[5]*a[27]-b[15]*a[31];
res[17]=b[17]*a[0]+b[26]*a[3]-b[28]*a[5]+b[31]*a[14]+b[0]*a[17]-b[3]*a[26]+b[5]*a[28]+b[14]*a[31];
res[18]=b[18]*a[0]+b[27]*a[3]+b[28]*a[4]-b[31]*a[13]+b[0]*a[18]-b[3]*a[27]-b[4]*a[28]-b[13]*a[31];
res[19]=b[19]*a[0]-b[26]*a[2]-b[29]*a[5]-b[31]*a[12]+b[0]*a[19]+b[2]*a[26]+b[5]*a[29]-b[12]*a[31];
res[20]=b[20]*a[0]-b[27]*a[2]+b[29]*a[4]+b[31]*a[11]+b[0]*a[20]+b[2]*a[27]-b[4]*a[29]+b[11]*a[31];
res[21]=b[21]*a[0]-b[28]*a[2]-b[29]*a[3]-b[31]*a[10]+b[0]*a[21]+b[2]*a[28]+b[3]*a[29]-b[10]*a[31];
res[22]=b[22]*a[0]-b[30]*a[5]+b[0]*a[22]+b[5]*a[30];
res[23]=b[23]*a[0]+b[30]*a[4]+b[0]*a[23]-b[4]*a[30];
res[24]=b[24]*a[0]-b[30]*a[3]+b[0]*a[24]+b[3]*a[30];
res[25]=b[25]*a[0]+b[30]*a[2]+b[0]*a[25]-b[2]*a[30];
res[26]=b[26]*a[0]+b[31]*a[5]+b[0]*a[26]+b[5]*a[31];
res[27]=b[27]*a[0]-b[31]*a[4]+b[0]*a[27]-b[4]*a[31];
res[28]=b[28]*a[0]+b[31]*a[3]+b[0]*a[28]+b[3]*a[31];
res[29]=b[29]*a[0]-b[31]*a[2]+b[0]*a[29]-b[2]*a[31];
res[30]=b[30]*a[0]+b[0]*a[30];
res[31]=b[31]*a[0]+b[0]*a[31];
res
}
}
// Add
// Multivector addition
impl Add for R401 {
type Output = R401;
fn add(self: R401, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]+b[0];
res[1] = a[1]+b[1];
res[2] = a[2]+b[2];
res[3] = a[3]+b[3];
res[4] = a[4]+b[4];
res[5] = a[5]+b[5];
res[6] = a[6]+b[6];
res[7] = a[7]+b[7];
res[8] = a[8]+b[8];
res[9] = a[9]+b[9];
res[10] = a[10]+b[10];
res[11] = a[11]+b[11];
res[12] = a[12]+b[12];
res[13] = a[13]+b[13];
res[14] = a[14]+b[14];
res[15] = a[15]+b[15];
res[16] = a[16]+b[16];
res[17] = a[17]+b[17];
res[18] = a[18]+b[18];
res[19] = a[19]+b[19];
res[20] = a[20]+b[20];
res[21] = a[21]+b[21];
res[22] = a[22]+b[22];
res[23] = a[23]+b[23];
res[24] = a[24]+b[24];
res[25] = a[25]+b[25];
res[26] = a[26]+b[26];
res[27] = a[27]+b[27];
res[28] = a[28]+b[28];
res[29] = a[29]+b[29];
res[30] = a[30]+b[30];
res[31] = a[31]+b[31];
res
}
}
// Sub
// Multivector subtraction
impl Sub for R401 {
type Output = R401;
fn sub(self: R401, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]-b[0];
res[1] = a[1]-b[1];
res[2] = a[2]-b[2];
res[3] = a[3]-b[3];
res[4] = a[4]-b[4];
res[5] = a[5]-b[5];
res[6] = a[6]-b[6];
res[7] = a[7]-b[7];
res[8] = a[8]-b[8];
res[9] = a[9]-b[9];
res[10] = a[10]-b[10];
res[11] = a[11]-b[11];
res[12] = a[12]-b[12];
res[13] = a[13]-b[13];
res[14] = a[14]-b[14];
res[15] = a[15]-b[15];
res[16] = a[16]-b[16];
res[17] = a[17]-b[17];
res[18] = a[18]-b[18];
res[19] = a[19]-b[19];
res[20] = a[20]-b[20];
res[21] = a[21]-b[21];
res[22] = a[22]-b[22];
res[23] = a[23]-b[23];
res[24] = a[24]-b[24];
res[25] = a[25]-b[25];
res[26] = a[26]-b[26];
res[27] = a[27]-b[27];
res[28] = a[28]-b[28];
res[29] = a[29]-b[29];
res[30] = a[30]-b[30];
res[31] = a[31]-b[31];
res
}
}
// smul
// scalar/multivector multiplication
impl Mul<R401> for float_t {
type Output = R401;
fn mul(self: float_t, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a*b[0];
res[1] = a*b[1];
res[2] = a*b[2];
res[3] = a*b[3];
res[4] = a*b[4];
res[5] = a*b[5];
res[6] = a*b[6];
res[7] = a*b[7];
res[8] = a*b[8];
res[9] = a*b[9];
res[10] = a*b[10];
res[11] = a*b[11];
res[12] = a*b[12];
res[13] = a*b[13];
res[14] = a*b[14];
res[15] = a*b[15];
res[16] = a*b[16];
res[17] = a*b[17];
res[18] = a*b[18];
res[19] = a*b[19];
res[20] = a*b[20];
res[21] = a*b[21];
res[22] = a*b[22];
res[23] = a*b[23];
res[24] = a*b[24];
res[25] = a*b[25];
res[26] = a*b[26];
res[27] = a*b[27];
res[28] = a*b[28];
res[29] = a*b[29];
res[30] = a*b[30];
res[31] = a*b[31];
res
}
}
// muls
// multivector/scalar multiplication
impl Mul<float_t> for R401 {
type Output = R401;
fn mul(self: R401, b: float_t) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]*b;
res[1] = a[1]*b;
res[2] = a[2]*b;
res[3] = a[3]*b;
res[4] = a[4]*b;
res[5] = a[5]*b;
res[6] = a[6]*b;
res[7] = a[7]*b;
res[8] = a[8]*b;
res[9] = a[9]*b;
res[10] = a[10]*b;
res[11] = a[11]*b;
res[12] = a[12]*b;
res[13] = a[13]*b;
res[14] = a[14]*b;
res[15] = a[15]*b;
res[16] = a[16]*b;
res[17] = a[17]*b;
res[18] = a[18]*b;
res[19] = a[19]*b;
res[20] = a[20]*b;
res[21] = a[21]*b;
res[22] = a[22]*b;
res[23] = a[23]*b;
res[24] = a[24]*b;
res[25] = a[25]*b;
res[26] = a[26]*b;
res[27] = a[27]*b;
res[28] = a[28]*b;
res[29] = a[29]*b;
res[30] = a[30]*b;
res[31] = a[31]*b;
res
}
}
impl Div<float_t> for R401 {
type Output = R401;
fn div(self: R401, b: float_t) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]/b;
res[1] = a[1]/b;
res[2] = a[2]/b;
res[3] = a[3]/b;
res[4] = a[4]/b;
res[5] = a[5]/b;
res[6] = a[6]/b;
res[7] = a[7]/b;
res[8] = a[8]/b;
res[9] = a[9]/b;
res[10] = a[10]/b;
res[11] = a[11]/b;
res[12] = a[12]/b;
res[13] = a[13]/b;
res[14] = a[14]/b;
res[15] = a[15]/b;
res[16] = a[16]/b;
res[17] = a[17]/b;
res[18] = a[18]/b;
res[19] = a[19]/b;
res[20] = a[20]/b;
res[21] = a[21]/b;
res[22] = a[22]/b;
res[23] = a[23]/b;
res[24] = a[24]/b;
res[25] = a[25]/b;
res[26] = a[26]/b;
res[27] = a[27]/b;
res[28] = a[28]/b;
res[29] = a[29]/b;
res[30] = a[30]/b;
res[31] = a[31]/b;
res
}
}
// sadd
// scalar/multivector addition
impl Add<R401> for float_t {
type Output = R401;
fn add(self: float_t, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a+b[0];
res[1] = b[1];
res[2] = b[2];
res[3] = b[3];
res[4] = b[4];
res[5] = b[5];
res[6] = b[6];
res[7] = b[7];
res[8] = b[8];
res[9] = b[9];
res[10] = b[10];
res[11] = b[11];
res[12] = b[12];
res[13] = b[13];
res[14] = b[14];
res[15] = b[15];
res[16] = b[16];
res[17] = b[17];
res[18] = b[18];
res[19] = b[19];
res[20] = b[20];
res[21] = b[21];
res[22] = b[22];
res[23] = b[23];
res[24] = b[24];
res[25] = b[25];
res[26] = b[26];
res[27] = b[27];
res[28] = b[28];
res[29] = b[29];
res[30] = b[30];
res[31] = b[31];
res
}
}
// adds
// multivector/scalar addition
impl Add<float_t> for R401 {
type Output = R401;
fn add(self: R401, b: float_t) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]+b;
res[1] = a[1];
res[2] = a[2];
res[3] = a[3];
res[4] = a[4];
res[5] = a[5];
res[6] = a[6];
res[7] = a[7];
res[8] = a[8];
res[9] = a[9];
res[10] = a[10];
res[11] = a[11];
res[12] = a[12];
res[13] = a[13];
res[14] = a[14];
res[15] = a[15];
res[16] = a[16];
res[17] = a[17];
res[18] = a[18];
res[19] = a[19];
res[20] = a[20];
res[21] = a[21];
res[22] = a[22];
res[23] = a[23];
res[24] = a[24];
res[25] = a[25];
res[26] = a[26];
res[27] = a[27];
res[28] = a[28];
res[29] = a[29];
res[30] = a[30];
res[31] = a[31];
res
}
}
// ssub
// scalar/multivector subtraction
impl Sub<R401> for float_t {
type Output = R401;
fn sub(self: float_t, b: R401) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a-b[0];
res[1] = -b[1];
res[2] = -b[2];
res[3] = -b[3];
res[4] = -b[4];
res[5] = -b[5];
res[6] = -b[6];
res[7] = -b[7];
res[8] = -b[8];
res[9] = -b[9];
res[10] = -b[10];
res[11] = -b[11];
res[12] = -b[12];
res[13] = -b[13];
res[14] = -b[14];
res[15] = -b[15];
res[16] = -b[16];
res[17] = -b[17];
res[18] = -b[18];
res[19] = -b[19];
res[20] = -b[20];
res[21] = -b[21];
res[22] = -b[22];
res[23] = -b[23];
res[24] = -b[24];
res[25] = -b[25];
res[26] = -b[26];
res[27] = -b[27];
res[28] = -b[28];
res[29] = -b[29];
res[30] = -b[30];
res[31] = -b[31];
res
}
}
// subs
// multivector/scalar subtraction
impl Sub<float_t> for R401 {
type Output = R401;
fn sub(self, b: float_t) -> R401 {
let mut res = R401::zero();
let a = self;
res[0] = a[0]-b;
res[1] = a[1];
res[2] = a[2];
res[3] = a[3];
res[4] = a[4];
res[5] = a[5];
res[6] = a[6];
res[7] = a[7];
res[8] = a[8];
res[9] = a[9];
res[10] = a[10];
res[11] = a[11];
res[12] = a[12];
res[13] = a[13];
res[14] = a[14];
res[15] = a[15];
res[16] = a[16];
res[17] = a[17];
res[18] = a[18];
res[19] = a[19];
res[20] = a[20];
res[21] = a[21];
res[22] = a[22];
res[23] = a[23];
res[24] = a[24];
res[25] = a[25];
res[26] = a[26];
res[27] = a[27];
res[28] = a[28];
res[29] = a[29];
res[30] = a[30];
res[31] = a[31];
res
}
}
impl R401 {
pub fn norm(self: Self) -> float_t {
let scalar_part = (self * self.conjugate())[0];
scalar_part.abs().sqrt()
}
pub fn inorm(self: Self) -> float_t {
self.dual().norm()
}
pub fn normalized(self: Self) -> Self {
self * (1.0 / self.norm())
}
pub fn commutator(self, mv: R401) -> Self { 0.5 * (self * mv - mv * self) }
}
fn main() {
println!("e0*e0 : {}", e0 * e0);
println!("pss : {}", e01234);
println!("pss*pss : {}", e01234*e01234);
}
Get Arbgeom beta
Arbgeom beta
Curved space marble game
| Status | In development |
| Author | Tomwol |
| Tags | bevy, marble-game, non-eucledian, non-euclidean |
More posts
- Some new Manifolds: Duocylinder & InterpolationMay 01, 2025
- Scripting files for Arbgeom, August 13, 2024Aug 14, 2024
Leave a comment
Log in with itch.io to leave a comment.